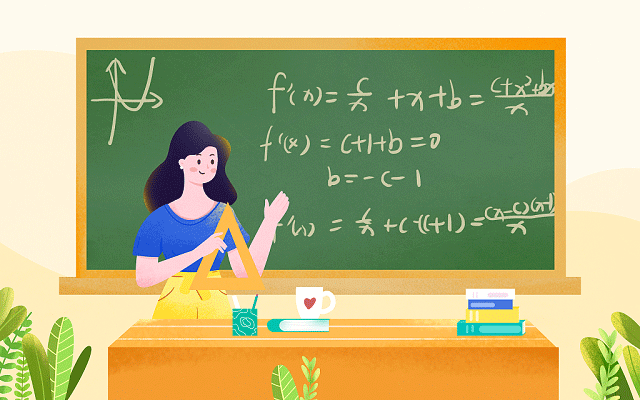分数列是数学中一种以分数形式排列的数列,其元素可以是任意的分数。根据数列的生成规则,分数列可分为以下几种类型:
等差分数列
每一项与前一项的差为常数。例如:$frac{1}{2}, frac{3}{2}, frac{5}{2}, dots$
通项公式:$a_n = a_1 + (n-1)d$(其中$a_1$为首项,$d$为公差)。
等比分数列
每一项与前一项的比值为常数。例如:$frac{1}{2}, frac{2}{4}, frac{4}{8}, dots$
通项公式:$a_n = a_1 cdot r^{n-1}$(其中$a_1$为首项,$r$为公比)。
任意分数数列
不满足等差或等比规律的分数序列,需通过其他方法(如数学归纳法)分析其特性。
补充说明
分数列的表示通常采用以下形式:
$$a_1, a_2, a_3, dots = frac{p_1}{q_1}, frac{p_2}{q_2}, frac{p_3}{q_3}, dots$$
其中$p_n$和$q_n$分别为第$n$项的分子和分母。
若需进行分数列的计算(如求和、通项公式推导),需根据具体类型选择合适的方法。例如,等比数列求和公式为:
$$S_n = a_1 cdot frac{1-r^n}{1-r} quad (r
eq 1)$$